New work provides a good view of where the field currently stands.
The first-generation tech demo of Atom’s hardware. Things have progressed considerably since. Credit: Atom Computing
In September, Microsoft made an unusual combination of announcements. It demonstrated progress with quantum error correction, something that will be needed for the technology to move much beyond the interesting demo phase, using hardware from a quantum computing startup called Quantinuum. At the same time, however, the company also announced that it was forming a partnership with a different startup, Atom Computing, which uses a different technology to make qubits available for computations.
Given that, it was probably inevitable that the folks in Redmond, Washington, would want to show that similar error correction techniques would also work with Atom Computing’s hardware. It didn’t take long, as the two companies are releasing a draft manuscript describing their work on error correction today. The paper serves as both a good summary of where things currently stand in the world of error correction, as well as a good look at some of the distinct features of computation using neutral atoms.
Atoms and errors
While we have various technologies that provide a way of storing and manipulating bits of quantum information, none of them can be operated error-free. At present, errors make it difficult to perform even the simplest computations that are clearly beyond the capabilities of classical computers. More sophisticated algorithms would inevitably encounter an error before they could be completed, a situation that would remain true even if we could somehow improve the hardware error rates of qubits by a factor of 1,000—something we’re unlikely to ever be able to do.
The solution to this is to use what are called logical qubits, which distribute quantum information across multiple hardware qubits and allow the detection and correction of errors when they occur. Since multiple qubits get linked together to operate as a single logical unit, the hardware error rate still matters. If it’s too high, then adding more hardware qubits just means that errors will pop up faster than they can possibly be corrected.
We’re now at the point where, for a number of technologies, hardware error rates have passed the break-even point, and adding more hardware qubits can lower the error rate of a logical qubit based on them. This was demonstrated using neutral atom qubits by an academic lab at Harvard University about a year ago. The new manuscript demonstrates that it also works on a commercial machine from Atom Computing.
Neutral atoms, which can be held in place using a lattice of laser light, have a number of distinct advantages when it comes to quantum computing. Every single atom will behave identically, meaning that you don’t have to manage the device-to-device variability that’s inevitable with fabricated electronic qubits. Atoms can also be moved around, allowing any atom to be entangled with any other. This any-to-any connectivity can enable more efficient algorithms and error-correction schemes. The quantum information is typically stored in the spin of the atom’s nucleus, which is shielded from environmental influences by the cloud of electrons that surround it, making them relatively long-lived qubits.
Operations, including gates and readout, are performed using lasers. The way the physics works, the spacing of the atoms determines how the laser affects them. If two atoms are a critical distance apart, the laser can perform a single operation, called a two-qubit gate, that affects both of their states. Anywhere outside this distance, and a laser only affects each atom individually. This allows a fine control over gate operations.
That said, operations are relatively slow compared to some electronic qubits, and atoms can occasionally be lost entirely. The optical traps that hold atoms in place are also contingent upon the atom being in its ground state; if any atom ends up stuck in a different state, it will be able to drift off and be lost. This is actually somewhat useful, in that it converts an unexpected state into a clear error.
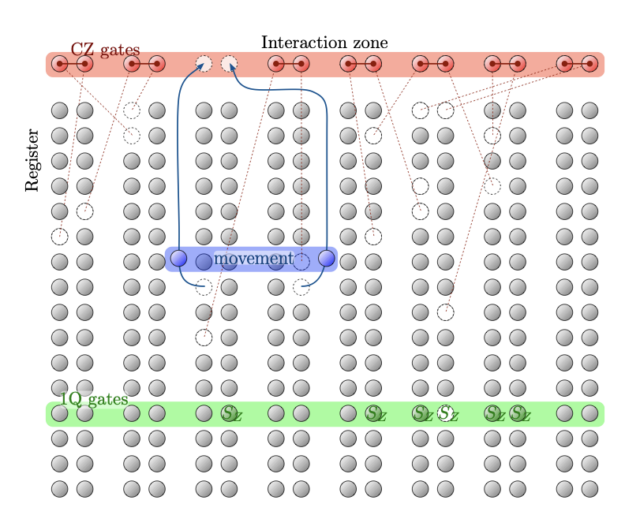
Atom Computing’s system. Rows of atoms are held far enough apart so that a single laser sent across them (green bar) only operates on individual atoms. If the atoms are moved to the interaction zone (red bar), a laser can perform gates on pairs of atoms. Spaces where atoms can be held can be left empty to avoid performing unneeded operations. Credit: Reichardt, et al.
The machine used in the new demonstration hosts 256 of these neutral atoms. Atom Computing has them arranged in sets of parallel rows, with space in between to let the atoms be shuffled around. For single-qubit gates, it’s possible to shine a laser across the rows, causing every atom it touches to undergo that operation. For two-qubit gates, pairs of atoms get moved to the end of the row and moved a specific distance apart, at which point a laser will cause the gate to be performed on every pair present.
Atom’s hardware also allows a constant supply of new atoms to be brought in to replace any that are lost. It’s also possible to image the atom array in between operations to determine whether any atoms have been lost and if any are in the wrong state.
It’s only logical
As a general rule, the more hardware qubits you dedicate to each logical qubit, the more simultaneous errors you can identify. This identification can enable two ways of handling the error. In the first, you simply discard any calculation with an error and start over. In the second, you can use information about the error to try to fix it, although the repair involves additional operations that can potentially trigger a separate error.
For this work, the Microsoft/Atom team used relatively small logical qubits (meaning they used very few hardware qubits), which meant they could fit more of them within 256 total hardware qubits the machine made available. They also checked the error rate of both error detection with discard and error detection with correction.
The research team did two main demonstrations. One was placing 24 of these logical qubits into what’s called a cat state, named after Schrödinger’s hypothetical feline. This is when a quantum object simultaneously has non-zero probability of being in two mutually exclusive states. In this case, the researchers placed 24 logical qubits in an entangled cat state, the largest ensemble of this sort yet created. Separately, they implemented what’s called the Bernstein-Vazirani algorithm. The classical version of this algorithm requires individual queries to identify each bit in a string of them; the quantum version obtains the entire string with a single query, so is a notable case of something where a quantum speedup is possible.
Both of these showed a similar pattern. When done directly on the hardware, with each qubit being a single atom, there was an appreciable error rate. By detecting errors and discarding those calculations where they occurred, it was possible to significantly improve the error rate of the remaining calculations. Note that this doesn’t eliminate errors, as it’s possible for multiple errors to occur simultaneously, altering the value of the qubit without leaving an indication that can be spotted with these small logical qubits.
Discarding has its limits; as calculations become increasingly complex, involving more qubits or operations, it will inevitably mean every calculation will have an error, so you’d end up wanting to discard everything. Which is why we’ll ultimately need to correct the errors.
In these experiments, however, the process of correcting the error—taking an entirely new atom and setting it into the appropriate state—was also error-prone. So, while it could be done, it ended up having an overall error rate that was intermediate between the approach of catching and discarding errors and the rate when operations were done directly on the hardware.
In the end, the current hardware has an error rate that’s good enough that error correction actually improves the probability that a set of operations can be performed without producing an error. But not good enough that we can perform the sort of complex operations that would lead quantum computers to have an advantage in useful calculations. And that’s not just true for Atom’s hardware; similar things can be said for other error-correction demonstrations done on different machines.
There are two ways to go beyond these current limits. One is simply to improve the error rates of the hardware qubits further, as fewer total errors make it more likely that we can catch and correct them. The second is to increase the qubit counts so that we can host larger, more robust logical qubits. We’re obviously going to need to do both, and Atom’s partnership with Microsoft was formed in the hope that it will help both companies get there faster.
John is Ars Technica’s science editor. He has a Bachelor of Arts in Biochemistry from Columbia University, and a Ph.D. in Molecular and Cell Biology from the University of California, Berkeley. When physically separated from his keyboard, he tends to seek out a bicycle, or a scenic location for communing with his hiking boots.
